ERF函数的定义与重要性
ERF函数,即误差函数(Error Function),在数学和工程领域中具有广泛的应用。ERF函数通常用于统计学、概率论以及物理学中的各种计算。其定义为:
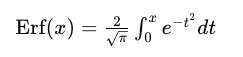
这一函数的主要用途是计算正态分布中的概率。正态分布是许多自然现象和统计数据的基础,ERF函数在其中起到了关键作用。由于其在误差理论中的重要性,ERF函数也被称为高斯误差函数。
ERF函数的应用不仅限于数学理论,还广泛应用于工程和科学研究中。例如,在信号处理、热传导和统计分析中,ERF函数都是不可或缺的工具。了解ERF函数的定义和重要性,有助于更好地理解其在各种科学和工程问题中的应用。
ERF函数在数学和物理中的应用
ERF函数在数学和物理学中的应用非常广泛。在数学中,ERF函数是解决积分方程和微分方程的重要工具。它在计算正态分布的累积分布函数(CDF)时尤为重要。正态分布的CDF可以通过ERF函数来表示:
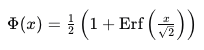
在物理学中,ERF函数常用于热传导和扩散过程的数学建模。例如,热方程的解可以通过ERF函数来表示,这对于理解材料在不同温度下的行为非常重要。热方程的一种解形式为:
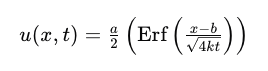
其中,k是热传导系数,a是初始温度,b是初始位置。
此外,ERF函数还在量子力学和电磁学中有所应用。例如,在量子力学中,ERF函数用于描述粒子的波函数,而在电磁学中,ERF函数用于计算电场和磁场的分布。
正态分布与ERF函数的关系
正态分布是统计学中最重要的分布之一,描述了许多自然现象和实验数据的分布情况。ERF函数与正态分布有着密切的关系,特别是在计算正态分布的累积分布函数(CDF)时。正态分布的CDF可以通过ERF函数来表示,这使得ERF函数在概率论和统计学中具有重要地位。
正态分布的概率密度函数(PDF)为:
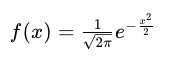
通过ERF函数,正态分布的CDF可以表示为:
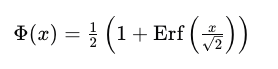
这一关系使得ERF函数成为计算正态分布概率的重要工具。无论是在统计分析还是在工程应用中,理解ERF函数与正态分布的关系都是至关重要的。
立即加入飞书 AI ready 计划,AI 时代快人一步 →
ERF函数与其他相关函数的联系
ERF函数与其他一些重要的数学函数有密切的联系。一个显著的例子是互补误差函数(Erfc),其定义为:
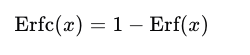
互补误差函数在计算高精度概率时非常有用,特别是在处理大数值时。由于ERF函数在大数值时接近1,直接计算可能导致精度损失,此时使用互补误差函数可以避免这一问题。
此外,ERF函数还与第一类合流超几何函数((_1F_1))有联系。在某些复杂积分中,ERF函数可以通过超几何函数来表示,这为求解复杂数学问题提供了更多工具。
通过理解ERF函数与其他相关函数的联系,可以更全面地掌握其在不同领域中的应用,从而在解决实际问题时更加得心应手。
ERF函数的计算方法
Maclaurin级数展开
ERF函数可以通过其Maclaurin级数展开来计算,这种方法在数学上非常经典。Maclaurin级数展开式为:
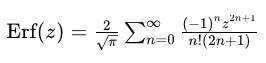
这种展开式在z值较小时非常有效,但当z值较大时,收敛速度较慢,因此在实际应用中可能需要结合其他方法。
数值积分方法
数值积分方法是计算ERF函数的另一种常用方法。通过数值积分,可以在计算机上高效地求解ERF函数的值。常见的数值积分方法包括梯形法、辛普森法以及高斯积分等。这些方法通过将积分区间分割成小段,并对每一小段进行近似计算,从而得到整个积分的近似值。
近似计算法
在实际应用中,常常需要快速计算ERF函数的近似值。以下公式可以作为该函数的良好近似,其准确度为107分之一:
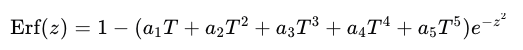
其中,T = 1 / (1 + 0.3275911 * z),a1, a2, a3, a4, a5为常数。这种近似计算法在工程应用中非常实用。
MATLAB与Excel中的ERF函数实现
在现代计算工具中,如MATLAB和Excel,都提供了内置的ERF函数计算功能。通过这些工具,可以方便地进行ERF函数的数值计算。
在MATLAB中,ERF函数的语法为:
erf(x)
例如,计算单个值的误差函数:
erf(0.76)
输出结果为:
ans = 0.7175
ERF函数在工程与科学研究中的应用
信号处理中的应用
在信号处理领域,ERF函数(误差函数erf)常用于分析和设计滤波器。由于ERF函数的积分性质,它在计算信号的累积分布和概率密度函数时非常有用。例如,在通信系统中,ERF函数被用来计算误码率(BER)。通过对高斯噪声进行分析,可以利用ERF函数来估计信号在噪声干扰下的误码概率。具体公式为:
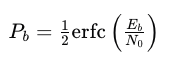
其中,(E_b) 是每比特的能量,(N_0) 是噪声功率谱密度。通过这种方式,工程师可以设计更加可靠的通信系统,确保数据在传输过程中的准确性。
统计学与概率论中的应用
ERF函数在统计学和概率论中也具有重要应用,特别是在处理正态分布时。正态分布是描述自然现象中随机变量的常用模型,而ERF函数则用于计算正态分布的累积分布函数(CDF)。具体来说,正态分布的CDF可以通过以下公式表示:
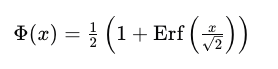
这一公式在统计分析中广泛应用,如在假设检验、置信区间估计等方面。通过ERF函数,统计学家可以更准确地描述数据分布,进行概率计算和推断。
热方程与扩散过程中的应用
在物理学中,ERF函数在热传导和扩散过程的数学建模中起到了关键作用。例如,热方程的解可以通过ERF函数来表示,这对于理解材料在不同温度下的行为非常重要。热方程的一种解形式为:

其中,(k) 是热传导系数,(a) 是初始温度,(b) 是初始位置。通过这种方式,科学家可以模拟和预测材料的温度分布和热传导行为,进而设计出更高效的热管理系统。
优化问题中的应用
在优化问题中,ERF函数也被广泛应用。特别是在机器学习和人工智能领域,ERF函数用于定义损失函数或误差函数。通过最小化这些误差函数,可以优化模型参数,提高模型的预测准确性。例如,在神经网络的训练过程中,ERF函数被用来计算预测值与实际值之间的误差,进而调整网络权重。
此外,ERF函数在金融工程、经济学等领域的优化问题中也有所应用。通过定义适当的误差函数,研究人员可以优化投资组合、风险管理策略等,提高经济效益和决策质量。
ERF函数与飞书功能的结合
在飞书表格、多维表格中,ERF 函数通常用来返回高斯误差函数的结果。这个函数是数学中的一个特殊函数,主要用于计算误差函数在上下限之间的积分。










